Recently, I implemented multiple gradentient descent-related optimization algorithms and applied to a simple loss function for visualization purpose.

The result look like such

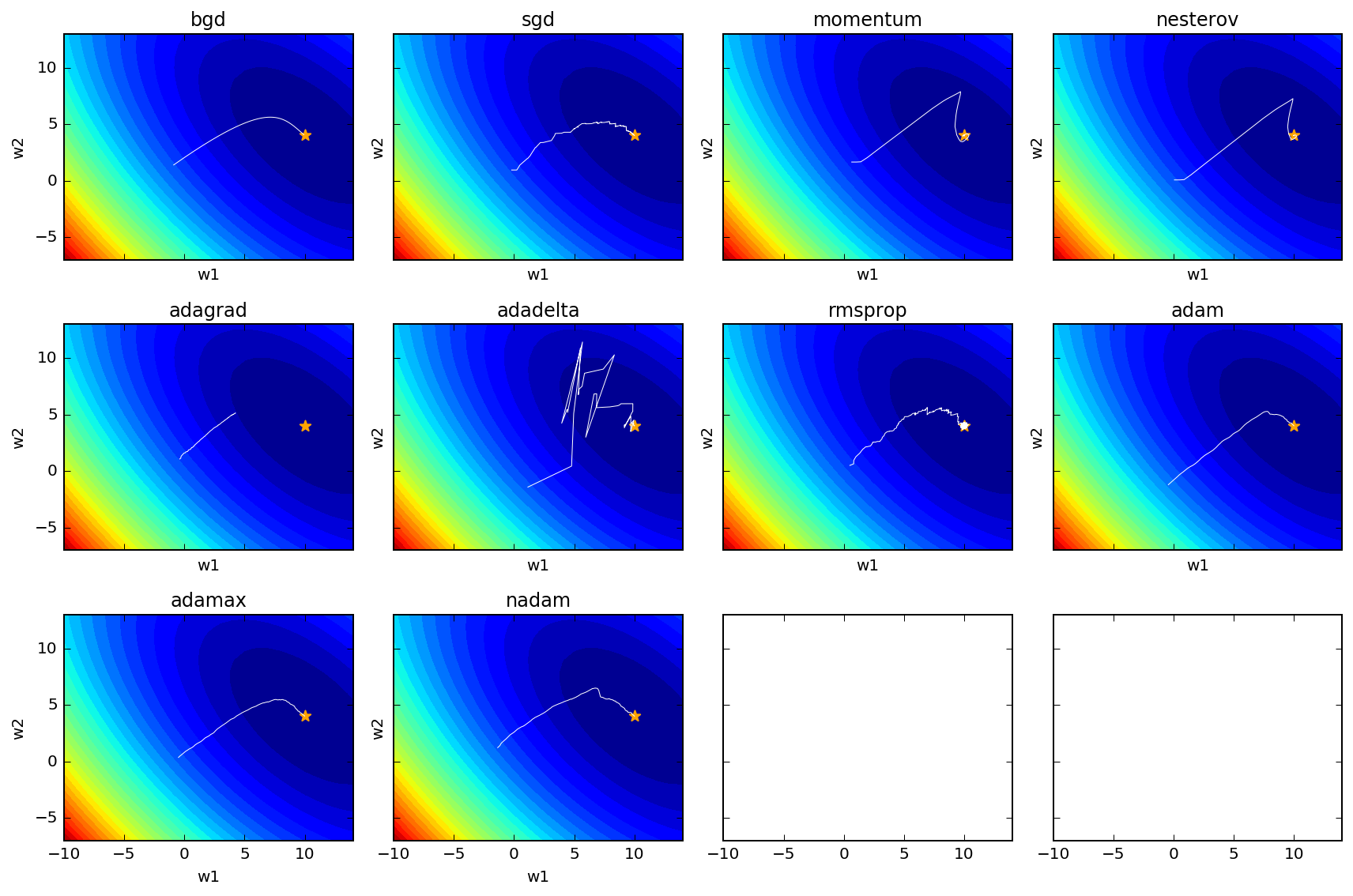
Legend:

  • The contour shows the surface of the loss function given the sampled data and the model function, a quadratic function with two parameters (w1 and w2).
  • The star indicates the true parameter of the quadratic function, from which the data is sampled.
  • The white line is the trajectory of gradient descent with the corresponding algorithm.

bgd: batch gradient descent; sgd: stochastic gradient descent.

Some comments:

  • Batch gradient descent is the most smooth
  • Stochastic gradient descent is more jumpy
  • Plain momentum and Nesterov accelerated momentum (NAM) overshoot and then correct themselve
  • Adagrad gets stuck as $G$ continues to increase adding squared gradients at each time step, effectively keeping reducing the learning rate to become infinitesimally small, thus learning gets halted.
  • Adadelta fixed the diminishing problem of Adagrad, resulting in very jumpy trajectories
  • RMSprop is quite similar to Adagrad, replacing $RMS[\Delta \theta]_{t-1}$ with $\eta$, but it doesn’t seem to be as good as Adadelta based on the above loss function trajectory.
  • Adam looks good.
  • AdaMax doesn’t look as good as Adam based on loss function
  • Nadam performs similar to Adam

For details, please see this notebooks and code in here.

Please let me know if you have any comment or bug report.