Here, I list some functions related to logistic regression that I get confused often.

Logit

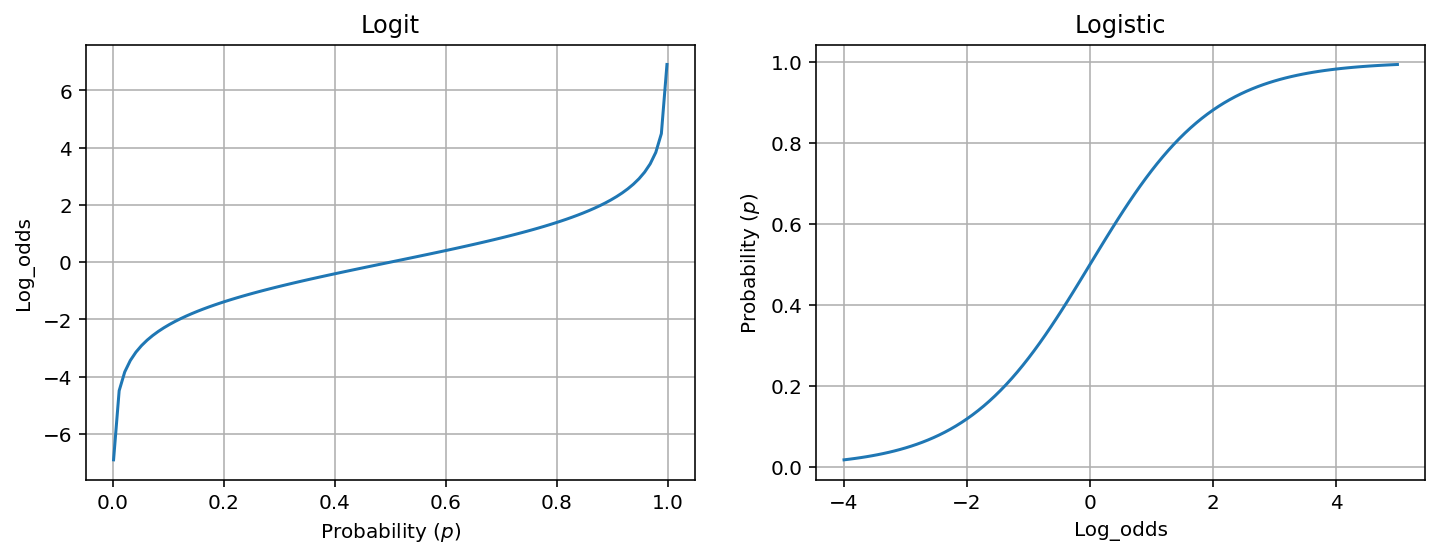
Logit function is basically the log of odds:

\[\begin{align} \text{logit}(p) = \log \frac{p}{1-p} \end{align}\]

where $p$ is a probability.

Logistic function

Logistic function is a common example of sigmoid function, which produces a S-shaped curve (aka. sigmoid curve).

\[\begin{align} f(x) = \frac{e^{x}}{1 + e^{x}} = \frac{1}{1 + e^{-x}} \label{eq:logistic} \end{align}\]

Some simple algebra shows that the logistic function is the inverse of the logit function (we use $p$ instead of $f(z)$ to be more intuitive as it relates to probability):

\[\begin{align} p &= \frac{e^x}{1 + e^x} \\ p + p e^x &= e^x \\ e^x &= \frac{p}{1-p} \\ x &= \log \frac{p}{1-p} \\ \end{align}\]

Note, $f(x)$ is commonly interpreted as a probability as it ranges from 0 (when $x \rightarrow -\infty$) to 1 (when $x \rightarrow \infty$).

In logistic regression, we are basically using a linear function of features to estimate the $x$, the log odds.

Softmax function

Softmax function is the extension of logistic function to more than two dimensions.

Suppose $\mathbf{z} = (z_1, \cdots, z_K) \in \mathbb{R}^K$.

\[\begin{align} p_k = f(z_k) = \frac{e^{z_k}}{\sum_{i=1}^{K} e^{z_i}} \end{align}\]

In a typical multiclass classification machine learn problem, $K$ dimensions correspond to $K$ categories, and each $f(z_k)$ can be interpreted as the probability of category $i$.

Note, adding a constant ($C$) to each $z_k$ won’t affect $f(z_k)$:

\[\begin{align} \frac{e^{z_k + C}}{\sum_{i=1}^{K} e^{z_i + C}} = \frac{e^C e^{z_k}}{e^C \sum_{i=1}^{K} e^{z_i}} = \frac{e^{z_k}}{\sum_{i=1}^{K} e^{z_i}} \end{align}\]

so for mathematical convenience, we can offset all components in $\mathbf{z}$ so that $z_k = 0$,

\[\begin{align} f(z_k) = \frac{e^{z_k - z_k}}{\sum_{i=1}^{K} e^{z_i - z_k}} = \frac{1}{1 + \sum_{i=1, i \neq k}^{K} e^{z_i - z_k}} \end{align}\]

In the case of $K=2$, let $k=1$, then softmax function becomes

\[\begin{align} f(z_1) = \frac{1}{1 + e^{z_2 - z_1}} = \frac{1}{1 + e^{- (z_1 - z_2)}} \label{eq:2d_softmax} \end{align}\]

which is equivalent to the logistic function Eq. \eqref{eq:logistic} with $x = z_1 - z_2$. Note, $z_k$ is often also referred to as “logit” in machine learning, but it cannot be interpreted as log odds as the logit in logistic function.

Dervie log odds from softmax

From the softmax function, we could derive the corresponding logit function for more than two dimensions.

\[\begin{align} p_k &= \frac{e^{z_k}}{\sum_{i=1}^{K} e^{z_i}} \\ p_k &= \frac{e^{z_k}}{e^{z_k} + \sum_{i \ne k}^{K} e^{z_i}} \\ p_k e^{z_k} + p_k \sum_{i \ne k}^{K} e^{z_i} &= e^{z_k} \\ e^{z_k} &= \frac{p_k \sum_{i \ne k}^{K} e^{z_i} }{1 - p_k} \\ z_k &= \log \frac{p_k \sum_{i \ne k}^{K} e^{z_i} }{1 - p_k} \\ z_k - \log \sum_{i \ne k}^{K} e^{z_i} &= \log \frac{p_k}{1 - p_k} \end{align}\]

So log odds of $p_k$ can be expressed as $z_k - \log \sum_{i \ne k}^{K} e^{z_i}$. Note, when $K = 2, k = 1$,

\[\begin{align} z_1 - z_2 = \log \frac{p(z_1)}{1 - p(z_1)} = x \end{align}\]

we just arrived at the same result as Eq. \eqref{eq:logistic} and Eq. \eqref{eq:2d_softmax}.