One dimension

When projecting a vector $\mathbf{x}$ onto another vector $\mathbf{u}$, denote the projected vector as $\alpha \mathbf{u}$, then $\alpha \mathbf{u} \perp \mathbf{x} - \alpha \mathbf{u}$.

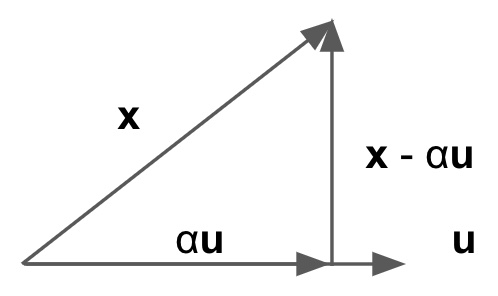
projection_proof_1D
Illustration of projection a vector $\mathbf{x}$ onto another vector $\mathbf{u}$.

Proof:

\[\begin{align*} \mathbf{u}^T (\mathbf{x} - \alpha \mathbf{u}) &= 0 \\ \alpha &= \frac{\mathbf{u}^T \mathbf{x}}{\mathbf{u}^T \mathbf{u}} \\ \alpha \mathbf{u} &= \frac{\mathbf{u} \mathbf{u}^T }{\mathbf{u}^T \mathbf{u}} \mathbf{x} = P \mathbf{x} \end{align*}\]

$P = \frac{\mathbf{u} \mathbf{u}^T }{\mathbf{u}^T \mathbf{u}}$ is known as the projection matrix. If $\mathbf{u}$ is of unit length, $P = \mathbf{u} \mathbf{u}^T$.

Multi-dimension

When projecting a vector $\mathbf{x}$ onto a matrix $A$, denote the projected vector as $A \mathbf{w}$, then $A \mathbf{w} \perp \mathbf{x} - A \mathbf{w}$. Note, $\mathbf{w}$ corresponds to the $\alpha$ in the 1D case, but $\mathbf{w}$ is a vector while $\alpha$ is a scalar.

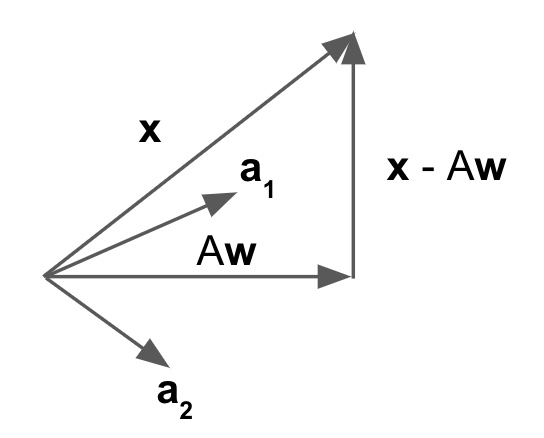
projection_proof_2D
Illustration of projection a vector $\mathbf{x}$ onto a matrix $A$ of two columns, $\mathbf{a}_1$ and $\mathbf{a}_2$.

Proof:

\[\begin{align*} A^T (\mathbf{x} - A \mathbf{w}) &= 0 \\ A^T \mathbf{x} &= A^T A \mathbf{w} \\ \mathbf{w} &= (A^T A)^{-1} A^T \mathbf{x} \\ A \mathbf{w} &= A (A^T A)^{-1} A^T \mathbf{x} = P \mathbf{x} \\ \end{align*}\]

$P = A (A^T A)^{-1} A^T$ is known as the projection matrix. If $A$ is orthonormal, then $P = A A^T$. Apparently, $P$ in the multi-dimensional case is just a generalization of the $P$ in the 1D case.